在进行系统的鲁棒优化学习之前,我们进行一些预备知识的回顾。本章将对线性规划、凸优化、锥优化以及风险偏好及其度量进行简要介绍。
2.1 线性规划概览(Linear optimization)
线性规划(LP)是数学规划中形式最为简单的一种模型。一个线性规划可以写作: $$ \begin{array}{rl} \min & \boldsymbol{c}^{\top} \boldsymbol{x} \\ {\rm s.t.} & \boldsymbol{A}\boldsymbol x \geq \boldsymbol{b}, \\ & \boldsymbol{x} \geq \boldsymbol{0}. \\ \end{array} $$ 可见上式中,目标函数和约束都是线性的形式,所以被叫做“线性规划”。虽然它的形式简单,但线性规划的建模能力非常强大,有很多经典的数学建模问题都可以转化为线性规划,也有很多非线性的函数也可以等价转化为线性规划求解。比如对于如下非线性的规划 $$ \begin{array}{rl} \min & f(\boldsymbol{x}) = \max\limits_{k} \left\{ \boldsymbol{d}^{\top}_k \boldsymbol{x} + c_k \right\} \\ {\rm s.t.} & \boldsymbol{A} \boldsymbol x \geq \boldsymbol{b}. \end{array} $$ 我们可以等价地将其转化为线性规划 $$ \begin{array}{rl} \min & z \\ {\rm s.t.} & \boldsymbol{A} \boldsymbol x \geq \boldsymbol{b}, \\ & z \geq \boldsymbol{d}^{\top}_k \boldsymbol{x} + c_k \quad \forall k. \\ \end{array} $$
当然,在实际解决过程的问题中要十分注意转化是否等价!一个常见的错误就是认为如下的两个数学规划问题是等价的。 $$ \begin{array}{rlrl} \min & \displaystyle\sum_{j\in [N]} c_j|x_j| \qquad \qquad \qquad & \min & \displaystyle \sum_{j\in [N]} c_jz_j\\ {\rm s.t.} & \boldsymbol{A} \boldsymbol x \geq \boldsymbol{b}. & {\rm s.t.} & \boldsymbol{A} \boldsymbol x \geq \boldsymbol{b}, \\ & & & x_j \geq - z_j, \\ & & & -x_j \geq -z_j. \\ \end{array} $$ 其实,当第一个规划问题有界,且存在$c_j<0$时,我们可以令线性规划中对应的$z_j\mapsto+\infty$,使得第二个问题最优值趋向于$-\infty$。此时易见两个问题并非等价。
说到数学规划问题,就不得不提到对偶(duality)理论。考虑一个(标准形式的)线性规划问题: $$ \begin{array}{rl} \min & \boldsymbol{c}^{\top}\boldsymbol x \\ {\rm s.t.} & \boldsymbol A \boldsymbol x = \boldsymbol b, \\ & \boldsymbol x \geq \boldsymbol 0. \end{array} $$ 我们可以使用拉格朗日乘子将上述问题写成: $$ \begin{array}{rl} g(\boldsymbol p) = \min & \boldsymbol{c}^{\top}\boldsymbol x + \boldsymbol p^{\top}( \boldsymbol b - \boldsymbol A \boldsymbol x)\\ {\rm s.t.}& \boldsymbol x \geq \boldsymbol 0. \end{array} $$ 令$\boldsymbol x^\ast$为线性规划的最优解,可见 $$ g(\boldsymbol p) \leq \boldsymbol c^{\top}\boldsymbol x^\ast + \boldsymbol p^{\top}( \boldsymbol b - \boldsymbol A \boldsymbol x^\ast) = \boldsymbol c^{\top} \boldsymbol x^\ast \quad \forall \boldsymbol p. $$ 也就是说,$ g(\boldsymbol p)$是最优目标函数$\boldsymbol c^\top \boldsymbol x^\ast $的一个下界。为了使这个下界尽可能的“紧”一些,我们想要求得$\displaystyle\max_{\boldsymbol p} g(\boldsymbol p)$: $$ g(\boldsymbol p)=\min_{\boldsymbol x \geq \boldsymbol 0}\ \boldsymbol c^{\top}\boldsymbol x + \boldsymbol p^{\top}(\boldsymbol b - \boldsymbol A \boldsymbol x) =\boldsymbol p^{\top}\boldsymbol b+\min_{\boldsymbol x\geq \boldsymbol 0}\ (\boldsymbol c - \boldsymbol A^{\top}\boldsymbol p)^{\top}\boldsymbol x. $$ 其中,我们有 $$ \min_{\boldsymbol x\geq \boldsymbol 0}\ (\boldsymbol c - \boldsymbol A^{\top}\boldsymbol p)^{\top}\boldsymbol x = \begin{cases} 0, & \mbox{如果 } \boldsymbol c^{\top} - \boldsymbol p^{\top}\boldsymbol A \geq \boldsymbol 0, \\ -\infty, & \text{否则}. \end{cases} $$ 至此,我们推出了原问题(primal)的对偶形式 $$ \begin{array}{rl} \max & \boldsymbol{b}^{\top}\boldsymbol p \\ {\rm s.t.} & \boldsymbol A^{\top} \boldsymbol p \leq \boldsymbol c. \\ \end{array} $$
关于原问题和对偶问题的关系,我们有弱对偶和强对偶两个定理。其中弱对偶表述的是:当$\boldsymbol x$是原问题的可行解且$\boldsymbol p$是对偶问题的可行解时,我们一定有$\boldsymbol b^{\top} \boldsymbol p\leq \boldsymbol c^{\top}\boldsymbol x$。也就是说原问题(min)的最优目标函数都要比对偶问题(max)最优目标函数要大。由此定理可知,如果我们能找到一组可行解$(\boldsymbol x,\boldsymbol p)$使得$\boldsymbol b^{\top} \boldsymbol p=\boldsymbol c^{\top} \boldsymbol x$,那么$\boldsymbol x$和$\boldsymbol p$就一定分别是原问题和对偶问题的最优解。值得一提的是,弱对偶对任意数学规划问题都成立。而强对偶表述的是:当线性规划有一个最优解时,那么它的对偶问题也有最优解,且两个问题的最优目标函数值相同。注意这里我们加上了线性规划这一条件。在更一般的凸优化中,我们必须要验证Slater condition来确认强对偶是否成立。关于线性规划的详细介绍,可以参阅Bertsimas and Tsitsiklis (1997)。
2.2 凸优化概览(Convex optimization)
虽然线性规划的建模能力十分强大,现实生活中很多非线性问题依然无法被LP解决。这个时候我们需要使用非线性规划(NLP)来求出最优解。一个非线性规划可以写作 $$ \begin{array}{rll} \min & f(\boldsymbol{x}) \\ {\rm s.t.} & g_i(\boldsymbol x) \leq 0 & \forall i=1 \in [m], \\ & h_i(\boldsymbol x) = 0 & \forall i \in [l]. \\ \end{array} $$ 其中,$f(\boldsymbol x):\mathbb R^n\mapsto\mathbb R$,$g_i(\boldsymbol x):\mathbb R^n\mapsto\mathbb R$和$h_i(\boldsymbol x):\mathbb R^n\mapsto\mathbb R$是关于$\boldsymbol x$的(通常连续且可微的)函数。
在非线性规划问题中,我们通常关注局部最优点和全局最优点。如果对于可行域中的$\boldsymbol x$,对于任意可行域中的$\boldsymbol y$都有$f(\boldsymbol x)\leq f(\boldsymbol y)$,那么$\boldsymbol x$就是全局最小。类似的,如果$f(\boldsymbol x)$比它周围的点都要小,那么$\boldsymbol x$是一个局部最小。(局部最小严格定义是,存在以$\boldsymbol x$为中心的一个开球,使得$f(\boldsymbol x)$比开球和可行域交集中所有可以取到的函数值都要小。)对于一个一般的非线性规划问题,我们通常很难验证一个点是局部最优还是全局最优。而如果一个非线性规划问题是凸优化问题,这个问题便迎刃而解。
具体来说,一个函数$f:S\mapsto R$如果满足$f(\lambda \boldsymbol x_1+(1-\lambda)\boldsymbol x_2)\leq \lambda f(\boldsymbol x_1)+(1-\lambda)f(\boldsymbol x_2)$,$\forall \lambda\in[0,1]$, $\boldsymbol x_1, \boldsymbol x_2\in S$,那么这个函数就被称为凸函数。在一个非线性规划问题中,如果$f(\boldsymbol x)$,$g(\boldsymbol x)$和$h(\boldsymbol x)$都为凸函数,那么这个NLP就是一个凸优化问题。
凸优化中一个重要的定理就是,如果$\boldsymbol x^\ast$是$f$的局部最小,那么$\boldsymbol x^\ast$也是$f$可行域中的全局最小。这个性质使得很多算法(例如各种迭代下降算法、内点算法等等)可以找到凸优化问题的全局最优解。我们也可以应用KKT条件来验证一个解是否为凸优化的问题的最优解。凸优化的详细介绍可以参阅Boyd and Vandenberghe (2004)。然而,在一个凸优化问题中,凸函数$f$,$g$和$h$的形式太过多元化。相比之下,任意一个线性规划都可以转化为标准形式(参见第 2.1节)。这样的标准形式可以大大减少推导鲁棒对等式(robust counterpart)时的步骤。那么一个凸优化问题可以转变为“标准形式”吗?为了达到这个目的,我们将在下节中介绍锥优化。
2.3 锥优化概览(Conic optimization)
沿用上节的符号系统,我们考虑目标函数$f(\boldsymbol x)$为线性形式的凸优化问题,即$f(\boldsymbol x)=\boldsymbol c^{\top} \boldsymbol x$。无论$g(\boldsymbol x)$和$h(\boldsymbol x)$形式如何,凸优化问题的可行域一定是一个凸集,写作$\mathcal X$。那么我们考虑的凸优化问题可以表示为: $$ \begin{array}{rcl} &\min & \boldsymbol c^{\top}\boldsymbol{x} \\ & {\rm s.t.} & \boldsymbol x \in \mathcal X. \\ \end{array} $$ 这个问题可以等价为如下规划问题 $$ \begin{array}{rcl} &\min & \boldsymbol c^{\top}\boldsymbol{x} \\ & {\rm s.t.} & y=1, \\ & & (\boldsymbol x,y)\in \mathcal K. \end{array} $$ 其中,$\mathcal K=\text{cl}\{ (\boldsymbol x,y):\boldsymbol x/y \in \mathcal X, y>0 \}$,$\text{cl}\{\cdot\}$表示一个集合的闭包。之所以写成这种形式,是因为$\mathcal K$是一种叫作“锥”的性质非常好的集合。我们把一个集合$\mathcal K$叫作锥,如果对任意的$\boldsymbol x\in \mathcal K$,$\lambda \boldsymbol x\in \mathcal K$对所有$\lambda \geq 0$都成立。
基于这个变换,第一个问题是:如何把线性规划和锥联系起来?第二个问题是:如果有办法联系起来,我们可以把线性规划的优良性质借鉴过来吗?我们先解决第一个问题——显然,非负$m$维实数域$\mathbb R_+^m$是一个锥。那么,我们可以把一个线性约束等价为 $$ \boldsymbol{A} \boldsymbol x \geq \boldsymbol b \Leftrightarrow \boldsymbol{A}\boldsymbol x - \boldsymbol b \geq \boldsymbol 0 \Leftrightarrow \boldsymbol{A}\boldsymbol x - \boldsymbol b \in \mathcal{K}, \quad \mathcal{K} = \mathbb{R}_{+}^{m}. $$ 而线性规划中很多非常好的数学性质来源于不等号“$\geq$”。具体来说,不等号满足
- 反射性(reflexibility):$\boldsymbol a \geq \boldsymbol a$;
- 反对称性(antisymmetry):如果$\boldsymbol a \geq \boldsymbol b$且$\boldsymbol b \geq \boldsymbol a$,那么$\boldsymbol a = \boldsymbol b$;
- 传递性(transitivity):如果$\boldsymbol a \geq \boldsymbol b$且$\boldsymbol b \geq \boldsymbol c$,那么$\boldsymbol a \geq \boldsymbol c$;
- 如果$\boldsymbol a \geq \boldsymbol b$,那么$\lambda \boldsymbol a \geq \lambda \boldsymbol b$对于所有$\lambda \geq 0$成立;
- 如果$\boldsymbol a \geq \boldsymbol b$且$\boldsymbol c\geq \boldsymbol d$,那么$\boldsymbol a+ \boldsymbol c \geq \boldsymbol b+ \boldsymbol d$。
基于这个观察,我们是否可以对于一个任意的锥$\mathcal K$,定义一个广义的不等式呢?答案是可以的。我们用“$\succeq_{\mathcal K}$”来定义如下的广义不等式关系: $$ \boldsymbol{A}\boldsymbol x \succeq_{\mathcal{K}} \boldsymbol{b} \Leftrightarrow \boldsymbol{A}\boldsymbol x - \boldsymbol{b} \succeq_{\mathcal{K}} \boldsymbol{0} \Leftrightarrow \boldsymbol{A}\boldsymbol x - \boldsymbol{b} \in \mathcal{K}, $$ $$ \boldsymbol{A}\boldsymbol x \succ_{\mathcal{K}} \boldsymbol{b} \Leftrightarrow \boldsymbol{A}\boldsymbol x - \boldsymbol{b} \succ_{\mathcal {K}} \boldsymbol{0} \Leftrightarrow \boldsymbol{A}\boldsymbol x - \boldsymbol{b} \in \mathrm{int} \mathcal{K}, $$ 其中, $\mathrm{int} \mathcal{K}$表示$\mathcal{K}$的内部(interior)。
可以证明,不等关系“$\succeq_{\mathcal K}$”同样继承了不等号“$\geq$”的上述所有性质。
基于这个推导,我们可以将一个(目标函数为线性函数)凸优化问题一般化为锥优化框架 $$ \begin{array}{lll} \min & \displaystyle \boldsymbol c^{\top} \boldsymbol x &\\ \text { s.t. } & \displaystyle \boldsymbol{A} \boldsymbol{x} = \boldsymbol b, \\ & \boldsymbol{x} \succeq_{\mathcal{K}} \boldsymbol{0}. \end{array} $$ 这个形式可以比作锥优化的“标准形式”。可见它和线性规划的标准形式有诸多相似之处。推导到这里,几个很自然的问题就是,这个问题的对偶形式是什么样的?强对偶在这个问题中成立吗?为了回答这些问题,首先引入对偶锥的概念。对于锥$\mathcal K$,它的对偶锥定义为 $$ \mathcal{K}^{\ast}=\left\{\boldsymbol{y} : \boldsymbol{y}^{\top} \boldsymbol{x} \geq 0, \quad \forall \boldsymbol{x} \in \mathcal{K}\right\}. $$ 有了这个定义,我们来推导锥优化的对偶问题。为了简单起见,我们忽略线性约束,考虑 $$ \begin{array}{rl} \min & \boldsymbol c^{\top} \boldsymbol x \\ \text { s.t. } & \boldsymbol{A}\boldsymbol x \succeq_{\mathcal {K}} \boldsymbol{b} \end{array} $$ 的对偶问题。
注意到,对任意的$\boldsymbol x \succeq_{K} \boldsymbol 0$和$\boldsymbol y \succeq_{K^{\ast}} \boldsymbol{0}$,我们有$\boldsymbol x^{\top} \boldsymbol y \geq 0$。
我们然后便可以引入拉格朗日乘子使问题等价于 $$ \min_{\boldsymbol x}\max_{\boldsymbol y\in \mathcal K^\ast}\ \boldsymbol c^{\top}\boldsymbol x+\boldsymbol y^{\top}(\boldsymbol b-\boldsymbol A\boldsymbol x). $$ 则对偶函数为 $$ \min_{\boldsymbol x}\ \boldsymbol c^{\top}\boldsymbol x+\boldsymbol y^{\top}(\boldsymbol b-\boldsymbol A\boldsymbol x)= \begin{cases} \boldsymbol b^{\top}\boldsymbol y, & \mbox{如果 } \boldsymbol A^{\top} \boldsymbol y=\boldsymbol c, \\ -\infty, & \text{否则}. \end{cases} $$ 在$\boldsymbol y\in\mathcal K^\ast$中最大化对偶函数,我们可以得到对偶问题 $$ \begin{array}{cl} \max & \boldsymbol b^{\top} \boldsymbol y\\ \text { s.t. } & \boldsymbol{A}^{\top}\boldsymbol{y} = \boldsymbol c, \\ & \boldsymbol y \succeq_{\mathcal {K}^{\ast}} \boldsymbol{0}. \end{array} $$
完成了对偶问题的推导,我们需要回答强对偶在这个问题中是否成立。简单来说,我们有如下结论。对于上述锥优化的“标准型”的原问题和对偶问题:
- 对偶问题的对偶问题等价于原问题。
- 对原问题可行的任意$\boldsymbol x$以及对对偶问题可行的任意$\boldsymbol y$,我们有$\boldsymbol c^{\top} \boldsymbol x \geq \boldsymbol b^{\top} \boldsymbol y$。
- 如果原问题有下界,且对某些$\boldsymbol x$有$\boldsymbol{A}\boldsymbol x - \boldsymbol b \in \mathrm{int} \mathcal K$严格成立,那么对偶问题可解,且原问题和对偶问题最优目标函数值相等。
- 如果原问题或对偶问题有界且严格可行($\boldsymbol{A}\boldsymbol x - \boldsymbol b \in \mathrm{int} \mathcal K$),$(\boldsymbol{x}, \boldsymbol{y})$是最优解与下列任意一条件等价:(i)$\boldsymbol c^{\top} \boldsymbol x = \boldsymbol b^{\top} \boldsymbol y$;或(ii)$\boldsymbol y^{\top}(\boldsymbol{A}\boldsymbol x - \boldsymbol b) = 0$。
2.4 风险偏好及度量(Risk preferences and risk measures)
本节主要介绍关于风险度量的基本知识。现实中,我们来决策做一件事(比如投资)时,在未来得到的回报往往都是不确定的。为了衡量一件事未来的风险和收益,人们引入了风险度量的概念。一件事的收益可以用随机变量来表示。同时,我们令$\mathcal V$为所有随机变量构成的空间,则其风险度量(risk measure)$\mu$需要满足两个特性:
- 单调性:对于任意的$\tilde r,\tilde s\in \mathcal V$且$\tilde r \geq \tilde s$, 那么$\mu[\tilde{r}] \leq \mu[\tilde{s}]$。这里,$\tilde r \geq \tilde s$表示的是state-wise dominance。
- 平移不变性:对于所有的$c\in \mathbb R$,$\mu[\tilde{r} + c] \leq \mu[\tilde{r}] - c$。
直观来说,单调性表示的意义为:当一件事未来的收益在任何可能性下都高于另一件事,那么它的风险一定是较小的。同时,平移不变性意味着:当一个资产确定性地增加了一定的价值,那么它的风险就会相应减少相同的数值。
基于上述定义,人们定义了非常多的风险度量。其中一个非常著名的风险度量就是在险价值(Value-at-Risk,VaR)。VaR的数学定义如下: $$ {\rm VaR}_\alpha[\tilde{r}] := \inf\left\{ m \in \mathbb{R} \mid \mathbb{P}[{ \tilde{r} + m \geq 0}] \geq 1-\alpha \right\}. $$
根据上述定义,VaR衡量了在给定概率$\alpha$下,一份投资可能的损失。例如,一个公司每个月在$\alpha=5\%$的VaR为一亿元。这意味着公司每个月都有5%的可能性损失超过一亿元。或者说,一个一亿元的损失平均每20个月就要发生一次。根据定义,我们同时可以将VaR和表示受益的随机变量$\tilde r$的分位数联系起来。下图显示,当一个随机变量5%的分位数为$-0.0263$时,对应的VaR的数值便为$0.0263$。
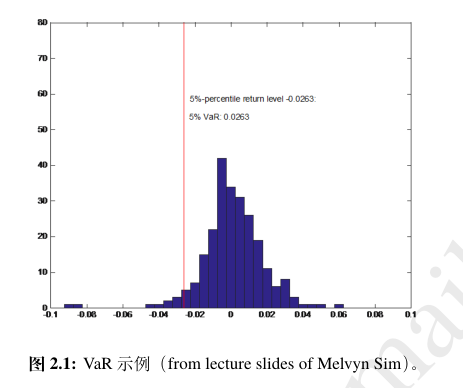
从上图同样能看出,VaR的取值只和单独的分位点值相关。而这样的性质会带来一些不便,比如对于有VaR介入的优化问题,通常来说都很难求解。同时,VaR在某些场合不能很好反应出不同投资的风险。假设我们有两种投资策略,其收益分别如下:
- 资产1:0.95概率收益200万,0.03概率损失100万,0.02概率损失200万;
- 资产2:0.95概率收益200万,0.03概率损失100万,0.02概率损失1000万。
显而易见资产2的风险比资产1更大,然而上述两个投资组合的VaR都是100万。为了解决这个问题,人们又提出了条件风险价值(Conditional Value-at-Risk,CVaR)的概念。CVaR计算了超过VaR值的可能损失的期望值,也就是说对于$\tilde r\sim \mathbb{P}$, $$ {\rm CVaR}^\ast_\alpha [\tilde{r}] \triangleq \mathbb{E}_{\mathbb{P}}[{-\tilde{r} \mid -\tilde{r} \geq {\rm VaR}_\alpha (\tilde{r}) }]. $$ 这里我们使用CVaR$^\ast$来表示CVaR,因为我们在后文中将推导出CVaR更常用的一个定义。为了区分,我们加上了一个星号上标。上述这个定义使得CVaR对于收益/损失的尾部分布的形状更加敏感。我们根据这个定义也可以看出${\rm CVaR}^\ast_\alpha [\tilde{r}] \geq {\rm VaR}_\alpha (\tilde{r})$。下图显示了CVaR和VaR的联系。我们也可以计算出在之前例子中,资产1的CVaR为140万,而资产2的CVaR为460万。
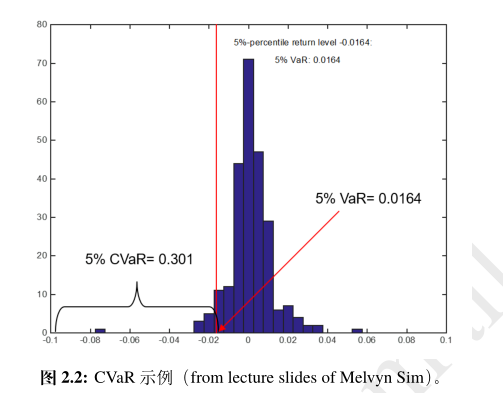
现在我们假设一项投资其未来的收益只能取$T$个可能的值$r_1,\ldots,r_{T}$。如果我们取$\alpha$使得$\alpha T$刚好为整数,那么CVaR可以等价地表达为 $$ {\rm CVaR}^\ast_\alpha [\tilde{r}] = \frac{1}{\alpha T} \max_{\mathcal{S} :~ \mathcal{S} \subseteq [T], \\ |\mathcal{S}| = \alpha T} \sum_{t \in \mathcal{S}} -r_t. $$ 但是这个定义并不通用,因为它不能定义当$\alpha T$不是整数的情况。为此,我们将推导出CVaR更通用的一个定义。注意到上式可等价地推出: $$ \begin{array}{rcll} {\rm CVaR}^\ast_\alpha [\tilde{r}] &=& \displaystyle \frac{1}{\alpha T} \max_{\mathcal{S} :~ \mathcal{S} \subseteq [T], \atop |\mathcal{S}| = \alpha T} \sum_{t \in \mathcal{S}} -r_t \\ &=& \displaystyle \frac{1}{\alpha T} \max_{\boldsymbol{z} \in \{0,1\}^T \atop \boldsymbol z^\top \boldsymbol 1 = \alpha T} \sum_{t \in [T]} -r_t z_t \\ &=& \displaystyle \frac{1}{\alpha T} \max_{\boldsymbol{z} \in [0,1]^T \atop \boldsymbol z^\top \boldsymbol 1 = \alpha T} \sum_{t \in [T] } -r_t z_t. \end{array} $$ 我们求出上述问题的对偶问题,得到 $$ \begin{array}{rcl} {\rm CVaR}_\alpha[\tilde{r}]=&\min & s + \frac{1}{\alpha T} \boldsymbol 1^\top \boldsymbol p \\ &{\rm s.t.}& s\boldsymbol 1 + \boldsymbol p \geq -\boldsymbol r, \\ & & \boldsymbol p \geq \boldsymbol 0, \end{array} $$ 即 $$ {\rm CVaR}_\alpha [\tilde{r}] = \inf_s \left\{s + \frac{1}{\alpha} \frac{1}{T}\sum_{t \in [T]}(-r_t - s)^+ \right\}. $$ 至此,当$\alpha T$不为整数时,我们可以根据上述推导定义CVaR为 $$ \begin{equation}\label{eq:cvar} {\rm CVaR}_\alpha [\tilde{r}] \triangleq \inf_v \left\{v + \frac{1}{\alpha}\mathbb{E}_{\mathbb{P}}[{ (-\tilde{r} - v)^+ }] \right\}. \tag{2.1} \end{equation} $$
这也是在优化领域中更常用的关于CVaR的定义。可以证明,在这个定义下依然有$\text{CVaR}_\alpha[\tilde{r}]\geq\text{VaR}_\alpha[\tilde{r}]$。
我们接下来介绍最优化确定等价收益(Optimized Certainty Equivalent,OCE)。对于不确定的收益$\tilde r$,定义其OCE为 (Ben-Tal and Teboulle, 2007) $$ S_u(\tilde r)=\sup_{\eta\in \mathbb{R}}\{ \eta+\mathbb{E}_{\mathbb{P}}[u(\tilde r - \eta)] \}. $$ 其中,$u: \mathbb{R}\mapsto \mathbb{R}$为非递减且凹的效用函数,并满足$u(0)=0$,且$1$是$u(r)$在$r=0$时的次梯度(subgradient)。我们可以通过公式这样解释OCE:一个决策者希望在未来有$\tilde r$的回报,而且在现在可以消费部分$\tilde r$。如果他在现在消费了确定的$\eta$的价值,那么$\tilde r$的现值就是$\eta+\mathbb{E}_{\mathbb{P}}[u(\tilde r - \eta)]$。对$\tilde r$进行现在和未来的最优分配,我们即可得到OCE。我们可以通过OCE来定义对应的风险度量。根据Ben-Tal and Teboulle (2007),$\mu^{OCE}[\tilde{r}]=-S_u(\tilde r)$是一个一致性风险度量(coherent risk measure)。为了把问题放进凸优化框架,我们记$v=-\eta$,$U(x)=-u(-x)$。此时$U:\mathbb R \mapsto \mathbb R$可以看做一个非递减的凸效用函数,而对应的风险度量表示为 $$ \mu^{OCE}[\tilde{r}] = \inf_{v \in \mathbb{R}}\left\{v + \mathbb{E}_{\mathbb{P}}[{U(-\tilde{r} -v)}] \right\}. $$ 对比式(2.1),我们可以看出CVaR是一种特殊的OCE度量,满足$U(r)=r^+/\alpha$。
在鲁棒优化领域,未来收益$\tilde r$的分布$\mathbb P$往往是不确定的。如果假设分布$\mathbb P$处于一个模糊集(ambiguity set)$\mathcal F$中,那么我们就可以写出在最坏情境(worst case)下对应的风险度量。以OCE举例,它在最坏情况下的风险度量写作 $$ \mu^{OCE}[\tilde{r}] = \inf_{v \in \mathbb{R}}\left\{v + \sup_{\mathbb{P} \in \mathcal{F}} \mathbb{E}_{\mathbb{P}}[{U(-\tilde{r} -v)} ] \right\}. $$ 这样决策优化问题就变成了一个分布鲁棒优化问题。关于分布鲁棒优化问题的求解,具体可以参见第4章。
我们最后介绍凸风险度量(convex risk measure)。对于一个风险度量$\mu$,它是凸风险度量当且仅当对于任意的$\tilde{r},\tilde{s} \in \mathcal{V}$,有 $$ \mu(\lambda \tilde{r} + (1-\lambda)\tilde{s} ) \leq \lambda \mu(\tilde{r}) + (1-\lambda)\mu(\tilde{s}). $$ 值得一提的是,OCE(包括CVaR)都是凸风险度量。而且,CVaR是所有凸风险度量中对VaR有最紧上界的一个,即如果$\mu[\tilde{r}] \geq {\rm VaR}_\alpha[\tilde{r}]$,$\forall \tilde{r} \in \mathcal{V}$,那么有$\mu[\tilde{r}] \geq {\rm CVaR}_\alpha[\tilde{r}] \geq {\rm VaR}_\alpha[\tilde{r}]$,$\forall \tilde{r} \in \mathcal{V}$。 另一个著名的凸风险度量是shortfall risk measure()。由于Föllmer and Schied, 2002篇幅所限不在此展开。有关于风险度量系统的知识,感兴趣的读者可以参阅Artzner et al. (1999) 和Föllmer and Schied (2002)。
参考文献
Artzner, Philippe, Freddy Delbaen, Jean-Marc Eber, and David Heath, “Coherent measures of risk,” Mathematical Finance, 1999, 9 (3), 203–228.
Ben-Tal, Aharon and Marc Teboulle, “An old-new concept of convex risk measures: the optimized certainty equivalent,” Mathematical Finance, 2007, 17 (3), 449–476.
Bertsimas, Dimitris and John N Tsitsiklis, Introduction to Linear Optimization, Athena Scientific Belmont, MA, 1997.
Boyd, Stephen and Lieven Vandenberghe, Convex Optimization, Cambridge university press, 2004.
Föllmer, Hans and Alexander Schied, “Convex measures of risk and trading constraints,” Finance and Stochastics, 2002, 6 (4), 429–447.